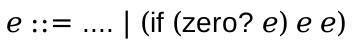15 Iniquity: function definitions and calls
15.1 Functions
With Hustle: heaps and lists, we removed a major computational shortcoming by adding the ability to use inductively defined data. Doing so gives programmers the ability to represent arbitrarily large pieces of information.
And yet, the language remains hamstrung. It has no mechanism to compute with such data. Sure, a programmer could compute the sum of the first n elements of a list, for some fixed n. But the size of this program would be proportional to the size of n. Want to compute the sum of a billion element list? You’ll need (at least) a billion expressions. Want to compute the sum of a larger list? Write a longer program! But if you want to compute the sum of any list, regardless of its size? You’ll need an arbitrarily long program. Of course programs are always of some fixed size, since after all, you have to write them down and at some point you have to stop writing. This means the expressiveness of our language is still severely restricted.
The solution is to bring in the computational analog of inductive data. When you have arbitrarily large data, you need arbitrarily long running computations to process them. Crucially, these arbitrarily long running computations need to be described by finite sized programs. The analog of inductive data are recursive functions.
So let’s now remove the computational shackles by incorporating functions, and in particular, recursive functions, which will allow us to compute over arbitrarily large data with finite-sized programs.
Let’s call it Iniquity.
We will extend the syntax by introducing a new syntactic category of programs, which consist of a sequence of function definitions followed by an expression:
(define (f₀ x₀₀ ...) e₀) (define (f₁ x₁₀ ...) e₁) ... e
And the syntax of expressions will be extended to include function calls:
(fᵢ e₀ ...)
where fᵢ is one of the function names defined in the program.
Note that functions can have any number of parameters and, symmetrically, calls can have any number of arguments. A program consists of zero or more function definitions followed by an expression.
An example concrete Iniquity program is:
#lang racket ;; Compute the length of the list (define (len xs) (if (empty? xs) 0 (add1 (len (cdr xs))))) (len (cons "a" (cons "b" (cons "c" '()))))
To represent these kinds of programs, we extend the definition of ASTs as follows:
#lang racket (provide Lit Prim0 Prim1 Prim2 Prim3 If Eof Begin Let Var Prog Defn App) ;; type Prog = (Prog (Listof Defn) Expr) (struct Prog (ds e) #:prefab) ;; type Defn = (Defn Id (Listof Id) Expr) (struct Defn (f xs e) #:prefab) ;; type Expr = (Lit Datum) ;; | (Eof) ;; | (Prim0 Op0) ;; | (Prim1 Op1 Expr) ;; | (Prim2 Op2 Expr Expr) ;; | (Prim3 Op3 Expr Expr Expr) ;; | (If Expr Expr Expr) ;; | (Begin Expr Expr) ;; | (Let Id Expr Expr) ;; | (Var Id) ;; | (App Id (Listof Expr)) ;; type ClosedExpr = { e ∈ Expr | e contains no free variables } ;; type Id = Symbol ;; type Datum = Integer ;; | Boolean ;; | Character ;; | '() ;; | String ;; type Op0 = 'read-byte | 'peek-byte | 'void ;; type Op1 = 'add1 | 'sub1 ;; | 'zero? ;; | 'char? | 'integer->char | 'char->integer ;; | 'write-byte | 'eof-object? ;; | 'car | 'cdr | 'unbox ;; | 'empty? | 'cons? | 'box? ;; | 'box ;; | 'vector? | 'vector-length ;; | 'string? | 'string-length ;; type Op2 = '+ | '- | '< | '= ;; | 'eq? | 'cons ;; | 'make-vector | 'vector-ref ;; | 'make-string | 'string-ref ;; type Op3 = 'vector-set! (struct Eof () #:prefab) (struct Lit (d) #:prefab) (struct Prim0 (p) #:prefab) (struct Prim1 (p e) #:prefab) (struct Prim2 (p e1 e2) #:prefab) (struct Prim3 (p e1 e2 e3) #:prefab) (struct If (e1 e2 e3) #:prefab) (struct Begin (e1 e2) #:prefab) (struct Let (x e1 e2) #:prefab) (struct Var (x) #:prefab) (struct App (f es) #:prefab)
The parser will need to be updated to parse programs, not just expressions. Since a program is a sequence of forms, we will assume the reader will read in all of these forms and construct a list of the elements. So the program parser parse takes a list of s-expressions. There is also a new parse for function definitions, parse-definition. The parser for expressions parse-e is updated to include function applications.
#lang racket (provide parse parse-closed parse-e parse-define) (require "ast.rkt") ;; [Listof S-Expr] -> Prog (define (parse . ss) (match (parse-prog ss (parse-defn-names ss) '() '() '()) [(list _ _ p) p])) ;; [Listof S-Expr] -> ClosedProg (define (parse-closed . ss) (match (parse-prog ss (parse-defn-names ss) '() '() '()) [(list '() '() p) p] [(list ys gs p) (error "undefined identifiers" (append ys gs))])) ;; S-Expr -> Expr ;; Parse a (potentially open) expression (define (parse-e s) (match (parse-e/acc s '() '() '() '()) [(list _ _ e) e])) ;; S-Expr -> Expr ;; Parse a (potentially open) definition (define (parse-define s) (match (parse-define/acc s '() '() '() '()) [(list _ _ d) d])) ;; S-Expr -> r:[Listof Id] ;; where: (distinct? r) ;; Extracts defined function names from given program-like s-expr ;; Does not fully parse definition ;; Example: ;; (parse-defn-names '((define (f x) x) (define (g y) y) 1) -> '(f g) (define (parse-defn-names ss) (define (rec ss fs) (match ss [(list s) fs] [(cons (cons 'define sd) sr) (match (parse-defn-name sd) [f (if (memq f fs) (error "duplicate definition" f) (rec sr (cons f fs)))])] [_ (error "parse error")])) (rec ss '())) (define (parse-defn-name s) (match s [(cons (cons (? symbol? f) _) _) f] [_ (error "parse error")])) ;; S-Expr [Listof Id] [Listof Id] [Listof Id] [Listof Id] -> (list [Listof Id] [Listof Id] Prog) ;; s: program shaped s-expr to be parsed ;; fs: defined function names ;; xs: bound variables ;; ys: free variables ;; gs: undefined function names ;; returns list of free variables, undefined function names, and parse of program (define (parse-prog s fs xs ys gs) (match s [(list s) (match (parse-e/acc s fs xs ys gs) [(list ys gs e) (list ys gs (Prog '() e))])] [(cons s ss) (match (parse-define/acc s fs xs ys gs) [(list ys gs (and d (Defn f _ _))) (match (parse-prog ss (cons f fs) xs ys gs) [(list ys gs (Prog ds e)) (list ys gs (Prog (cons d ds) e))])])])) ;; S-Expr [Listof Id] [Listof Id] [Listof Id] [Listof Id] -> (list [Listof Id] [Listof Id] Defn) ;; s: definition shaped s-expr to be parsed ;; fs: defined function names ;; xs: bound variables ;; ys: free variables ;; gs: undefined function names ;; returns list of free variables, undefined function names, and parse of definition (define (parse-define/acc s fs xs ys gs) (match s [(cons 'define sr) (match sr [(list (cons (? symbol? g) (and (list (? symbol? zs) ...) (? distinct?))) s) (match (parse-e/acc s (cons g fs) (append zs xs) ys gs) [(list ys gs e) (list ys gs (Defn g zs e))])] [_ (error "parse error")])] [_ (error "parse error")])) ;; S-Expr [Listof Id] [Listof Id] [Listof Id] [Listof Id] -> (list [Listof Id] [Listof Id] Expr) ;; s: expression shaped s-expr to be parsed ;; fs: defined function names ;; xs: bound variables ;; ys: free variables ;; gs: undefined function names ;; returns list of free variables, undefined function names, and parse of expression (define (parse-e/acc s fs xs ys gs) (define (rec s xs ys gs) (define ns (append fs xs)) (match s [(and 'eof (? (not-in ns))) (list ys gs (Eof))] [(? datum?) (list ys gs (Lit s))] [(list 'quote (list)) (list ys gs (Lit '()))] [(? symbol? (? (not-in fs))) (if (memq s xs) (list ys gs (Var s)) (list (cons s ys) gs (Var s)))] [(list-rest (? symbol? (? (not-in ns) k)) sr) (match k ['let (match sr [(list (list (list (? symbol? x) s1)) s2) (match (rec s1 xs ys gs) [(list ys gs e1) (match (rec s2 (cons x xs) ys gs) [(list ys gs e2) (list ys gs (Let x e1 e2))])])] [_ (error "let: bad syntax" s)])] [_ (match (parse-es/acc sr fs xs ys gs) [(list ys gs es) (match (cons k es) [(list (? op0? o)) (list ys gs (Prim0 o))] [(list (? op1? o) e1) (list ys gs (Prim1 o e1))] [(list (? op2? o) e1 e2) (list ys gs (Prim2 o e1 e2))] [(list (? op3? o) e1 e2 e3) (list ys gs (Prim3 o e1 e2 e3))] [(list 'begin e1 e2) (list ys gs (Begin e1 e2))] [(list 'if e1 e2 e3) (list ys gs (If e1 e2 e3))] [(list-rest g es) (list ys (cons g gs) (App g es))])])])] [(list-rest (? symbol? g) sr) (match (parse-es/acc sr fs xs ys gs) [(list ys s es) (list ys (if (memq g fs) gs (cons g gs)) (App g es))])] [_ (error "parse error" s)])) (rec s xs ys gs)) ;; S-Expr [Listof Id] [Listof Id] [Listof Id] [Listof Id] -> (list [Listof Id] [Listof Id] [Listof Expr]) ;; s: list of expressions shaped s-expr to be parsed ;; fs: defined function names ;; xs: bound variables ;; ys: free variables ;; gs: undefined function names ;; returns list of free variables, undefined function names, and list of parsed expressions (define (parse-es/acc s fs xs ys gs) (match s ['() (list ys gs '())] [(cons s ss) (match (parse-e/acc s fs xs ys gs) [(list ys gs e) (match (parse-es/acc ss fs xs ys gs) [(list ys gs es) (list ys gs (cons e es))])])] [_ (error "parse error")])) ;; [Listof Any] -> Boolean (define (distinct? xs) (not (check-duplicates xs))) ;; xs:[Listof Any] -> p:(x:Any -> Boolean) ;; Produce a predicate p for things not in xs (define (not-in xs) (λ (x) (not (memq x xs)))) (define (in m) (λ (x) (memq x m))) ;; Any -> Boolean (define (self-quoting-datum? x) (or (exact-integer? x) (boolean? x) (char? x) (string? x))) ;; Any -> Boolean (define (datum? x) (or (self-quoting-datum? x) (empty? x))) ;; Any -> Boolean (define (op0? x) (memq x '(read-byte peek-byte void))) (define (op1? x) (memq x '(add1 sub1 zero? char? integer->char char->integer write-byte eof-object? box unbox empty? cons? box? car cdr vector? vector-length string? string-length))) (define (op2? x) (memq x '(+ - < = eq? cons make-vector vector-ref make-string string-ref))) (define (op3? x) (memq x '(vector-set!)))
Because of the change from a program being a single expression to a sequence, we have to update the utilities that read program files, i.e. interp-stdin.rkt and compile-stdin.rkt:
#lang racket (provide main) (require "parse.rkt") (require "interp.rkt") (require "read-all.rkt") ;; -> Void ;; Parse and interpret contents of stdin, ;; print result on stdout (define (main) (read-line) ; ignore #lang racket line (println (interp (apply parse-closed (read-all)))))
15.2 An Interpreter for Functions
Writing an interpreter for Iniquity is not too hard. The main idea is that the interpretation of expression is now parameterized by a set of function definitions from the program. It serves as a second kind of environment that gets passed around and is used to resolve function definitions when interpreting function calls.
The way a function call is interpreted is to first interpret all of the arguments, building up a list of results. Then the definition of the function being called is looked up. If the function has the same number of parameters as there are arguments in the call, the body of the function is interpreted in an enviorment that maps each parameter to to the corresponding argument. That’s it.
#lang racket (provide interp interp-e) (require "ast.rkt") (require "interp-prim.rkt") (require "env.rkt") ;; type Value = ;; | Integer ;; | Boolean ;; | Character ;; | Eof ;; | Void ;; | '() ;; | (cons Value Value) ;; | (box Value) ;; | (string Character ...) ;; | (vector Value ...) ;; type Answer = Value | 'err ;; type Env = (Listof (List Id Value)) (define (err? x) (eq? x 'err)) ;; ClosedExpr -> Answer ;; Prog -> Answer (define (interp p) (with-handlers ([err? identity]) (match p [(Prog ds e) (interp-e e '() ds)]))) ;l Expr Env Defns -> Value { raises 'err } (define (interp-e e r ds) ;; where r closes e (match e [(Var x) (lookup r x)] [(Lit d) d] [(Eof) eof] [(Prim0 p) (interp-prim0 p)] [(Prim1 p e) (interp-prim1 p (interp-e e r ds))] [(Prim2 p e1 e2) (interp-prim2 p (interp-e e1 r ds) (interp-e e2 r ds))] [(Prim3 p e1 e2 e3) (interp-prim3 p (interp-e e1 r ds) (interp-e e2 r ds) (interp-e e3 r ds))] [(If e1 e2 e3) (if (interp-e e1 r ds) (interp-e e2 r ds) (interp-e e3 r ds))] [(Begin e1 e2) (begin (interp-e e1 r ds) (interp-e e2 r ds))] [(Let x e1 e2) (let ((v (interp-e e1 r ds))) (interp-e e2 (ext r x v) ds))] [(App f es) (let ((vs (interp-e* es r ds))) (match (defns-lookup ds f) [(Defn f xs e) ; check arity matches (if (= (length xs) (length vs)) (interp-e e (zip xs vs) ds) (raise 'err))]))])) ;; (Listof Expr) REnv Defns -> (Listof Value) { raises 'err } (define (interp-e* es r ds) (match es ['() '()] [(cons e es) (cons (interp-e e r ds) (interp-e* es r ds))])) ;; Defns Symbol -> Defn (define (defns-lookup ds f) (findf (match-lambda [(Defn g _ _) (eq? f g)]) ds)) (define (zip xs ys) (match* (xs ys) [('() '()) '()] [((cons x xs) (cons y ys)) (cons (list x y) (zip xs ys))]))
A couple of things to note:
since the function definition environment is passed along even when interpreting the body of function definitions, this interpretation supports recursion, and even mutual recursion.
functions are not values (yet). We cannot bind a variable to a function. We cannot make a list of functions. We cannot compute a function. The first position of a function call is a function name, not an arbitrary expression. Nevertheless, we have significantly increased the expressivity of our language.
We can try it out:
Examples
> (interp (parse '(define (double x) (+ x x)) '(double 5))) 10
We can see it works with recursive functions, too. Here’s a recursive function for computing triangular numbers:
Examples
> (interp (parse '(define (tri x) (if (zero? x) 0 (+ x (tri (sub1 x))))) '(tri 9))) 45
We can even define mutually recursive functions such as even? and odd?:
Examples
> (interp (parse '(define (even? x) (if (zero? x) #t (odd? (sub1 x)))) '(define (odd? x) (if (zero? x) #f (even? (sub1 x)))) '(even? 101))) #f
And the utility for interpreting programs in files works as well:
shell
> cat example/len.rkt | racket -t interp-stdin.rkt -m 3
15.3 Conventions of Calling
We’ve seen how to make calls in assembly already and our compiler emits code to call functions defined in C in our runtime such write_byte and read_byte. Let’s review the basics.
Suppose we want a function that does the same thing as (define (dbl x) (+ x x)). We can implement it in assembly with a labelled block of code:
(seq (Label 'dbl) (Mov 'rax (Offset 0 'rsp)) (Add 'rax 'rax) (Ret))
This function expects its argument to be available as the first position on the stack. That’s different from the calling convention defined by the System V ABI and used to call C code, but we can make our conventions for our language, so long as we’re mindful of respecting the System V ABI when interacting with code generated by other compilers (e.g. gcc).
So under a calling convention in which arguments are passed on the stack, a caller should push a value for the argument before calling the function and then pop it off after the function call returns:
(seq (%%% "Calling dbl(5)") (Mov 'rax 5) (Push 'rax) (Call 'dbl) ; rax holds 10 now ; pop the argument (Add rsp 8))
This almost works, but has a crucial flaw. The problem is that Call is an instruction that pushes on the stack. It pushes the return address, i.e. the location of the instruction the function should return to when it’s done, which will be located in (Offset 'rsp 0) when control jumps to (Label 'dbl). That means that the argument will be in (Offset 'rsp 8).
So we can touch-up the example as follows and it will work:
Examples
> (asm-interp (seq (Global 'entry) (Label 'entry) (%%% "Calling dbl(5)") (Mov 'rax 5) (Push 'rax) (Call 'dbl) ; rax holds 10 now ; pop the argument (Add rsp 8) (Ret) (Label 'dbl) (Mov 'rax (Offset 'rsp 8)) (Add 'rax 'rax) (Ret))) 10
One of the unfortunate things about this set-up is that the code for dbl has to “skip” past the return pointer on the stack to access the arguments.
Think for a moment about a call in Racket:
(define (dbl x) (+ x x)) (dbl 5)
Once the function call has fully evaluated it’s arguments (in this case the argument is a literal, so it’s already evaluated), then it should evaluate the body of the called function in an environment in which the parameter (here: x) is bound to the argument (5), hence (dbl 5) is equivalent to:
(let ((x 5)) (+ x x))
The problem with this perspective on function calls is that it doesn’t work well with the Call instruction pushing the return pointer on as the top frame of the stack before jumping to the function body. In the let-expression, x occurs at lexical address 0, but because of the return address being on the stack, the value of x is really at (Offset 'rsp 8).
We can fix this, but let’s recall that Call can be expressed
in terms of more primitive instructions: all a call is doing is
computing the return address—
We can do this ourselves, although we will need to use a new instruction: Lea:
(seq (%%% "Calling dbl(5)") (Mov 'rax 5) (Push 'rax) ; Call 'dbl but without using Call (let ((rp (gensym))) (seq (Lea 'rax rp) (Push 'rax) (Jmp 'dbl) (Label rp))) ; rax holds 10 now ; pop the argument (Add rsp 8) (Ret))
The Lea instruction is the “load effective address” instruction; it can compute the location of a given label. Here we are labelling the spot immediately after the jump to dbl, which is where we’d like the function call to return to.
We can verify this works just like before:
Examples
> (asm-interp (seq (Global 'entry) (Label 'entry) (%%% "Calling dbl(5)") (Mov 'rax 5) (Push 'rax) ; Call but without using Call (let ((rp (gensym))) (seq (Lea 'rax rp) (Push 'rax) (Jmp 'dbl) (Label rp))) ; rax holds 10 now ; pop the argument (Add rsp 8) (Ret) (Label 'dbl) (Mov 'rax (Offset 'rsp 8)) (Add 'rax 'rax) (Ret))) 10
What’s nice about expressing things in their more primitive form is we can now change the way in which calls are made. For example, we can now push the address on the stack before the arguments:
(seq (%%% "Calling dbl(5)") ; Call 'dbl but without using Call (let ((rp (gensym))) (seq (Lea 'rax rp) (Push 'rax) ; push return address (Mov 'rax 5) (Push 'rax) ; *then* push argument (Jmp 'dbl) (Label rp))) ; rax holds 10 now ; pop the argument (Add rsp 8) (Ret))
This way the called function can fetch variable bindings by their lexical address, i.e. x will be at (Offset rsp 0).
The problem now is that the called function doesn’t have the return address at the top off the stack when it does its Ret, rather it has the value of its argument.
But the function knows how many arguments it takes and these arguments will be popped by the caller as soon as the function returns, so here’s an idea: let’s have the called function pop the arguments off. (Note that this is just like how let works: it pops its bindings off after the body is done.) After the arguments are popped, where is the return address on the stack? (Offset 'rsp 0). So after the arguments are popped, (Ret) works as expected.
Here’s a complete version where the caller no longer pops the arguments but instead leaves it up to the function:
Examples
> (asm-interp (seq (Global 'entry) (Label 'entry) (%%% "Calling dbl(5)") ; Call but without using Call (let ((rp (gensym))) (seq (Lea 'rax rp) (Push 'rax) ; push return address (Mov 'rax 5) (Push 'rax) ; *then* push argument (Jmp 'dbl) (Label rp))) ; rax holds 10 now ; no need to pop argument (Ret) (Label 'dbl) (Mov 'rax (Offset 'rsp 0)) ; x is at offset 0 now (Add 'rax 'rax) (Add 'rsp 8) ; pop argument off (Ret))) 10
It works as expected.
Let’s use this as the basis of our calling convention.
A function call should:
Push a return address on the stack
Push all of the arguments on the stack
Jump to the function
The call will jump to the return address with all of these item popped off the stack.
A function should:
Access arguments on the stack, starting from offset 0
Before returning, pop all of the arguments on the stack
Then return
You may notice that things will go wrong if a call pushes a number of arguments that doesn’t match the number of parameters to the function, e.g. compiling something like:
(define (dbl x) (+ x x)) (dbl 1 2 3)
In Iniquity, it’s possible to statically determine whether the function call’s number of arguments match the function’s number of parameters and we can consider mismatches as syntax errors (and thus our compiler need not worry about this happening). In more expressive languages, this won’t be the case, but we can consider how to check that these two numbers match at run-time. For now, let’s not worry about it.
15.4 Compiling Function Calls and Definitions
With our calling convention in place, it’s pretty easy to compile function definitions and function calls. A function definition:
(define (f x ...) e)
Should be compiled as:
(seq (Label f) (compile-e e (list x ...)) (Add 'rsp (* 8 (length (list x ....)))) (Ret))
This creates a label based on the function’s name. The body of the function is compiled in an environment in which all of the parameters are bound. After the body executes, all of the arguments are popped from the stack, leaving the return address at the top of the stack, at which point the function returns.
For a function call:
(f e0 ...)
We can uses the following helper for compiling a sequence of expressions and pushing their values on the stack:
; [Listof Expr] CEnv -> Asm (define (compile-es es c) (match es ['() '()] [(cons e es) (seq (compile-e e c) (Push rax) (compile-es es (cons #f c)))]))
Using this, the call can be compiled as:
(let ((r (gensym 'ret))) (seq (Lea rax r) (Push rax) (compile-es es (cons #f c)) (Jmp (symbol->label f)) (Label r)))
Notice that we compile es in a static environment that is one frame larger than that of the call because we have pushed the return address on the stack and need to adjust the offsets of variable references in es.
It’s convenient that we evaluate es, saving the results to the stack, which is just where they need to be in order to make the function call. There is a subtle problem with this code though: compile-es generates code to execute the expression in es from left to right, pushing to the stack along the way. Thus the last argument will be the first element of the stack and the first argument will be the furthest element. That suggests we should compile the body of a function with its parameter list reversed so that the last parameter is at offset 0 and its first parameter is as (sub1 n) where n is the number of parameters. Touching up the code, we compile function definitions as:
(seq (Label f) (compile-e e (reverse (list x ...))) (Add 'rsp (* 8 (length (list x ....)))) (Ret))
Now writing the complete definitions for compile-define and compile-app, we have:
; Defn -> Asm (define (compile-define d) (match d [(Defn f xs e) (seq (Label f) (compile-e e (reverse xs)) (Add rsp (* 8 (length xs))) (Ret))])) ; Id [Listof Expr] CEnv -> Asm (define (compile-app f es c) (let ((r (gensym 'ret))) (seq (Lea rax r) (Push rax) (compile-es es (cons #f c)) (Jmp (symbol->label f)) (Label r))))
15.5 On Names and Labels
There is one final wrinkle, which is that identifiers in our language include many things which are not valid labels for the Nasm assembler. Hence compiling a function like:
(define (^weird% x) x)
will cause the assembler to reject the emitted code since '^weird% is not a valid label name. Labels must consist only of letters, numbers, _, $, ?, @, ~, and ?.
We solve this problem by using a function that maps arbitrary Racket symbols to valid Nasm labels (represented as symbols). The function has the property distinct symbols always map to distinct labels.
Examples
> (symbol->label '^weird%) 'label__weird__c3e020e4e5471e4
Using this function, we can touch up our code:
; Defn -> Asm (define (compile-define d) (match d [(Defn f xs e) (seq (Label (symbol->label f)) (compile-e e (reverse xs)) (Add rsp (* 8 (length xs))) (Ret))]))
15.6 A Compiler for Iniquity
The last piece of the puzzle is the function for emitting code for a complete program:
; Prog -> Asm (define (compile p) (match p [(Prog ds e) (prog (externs) (Global 'entry) (Label 'entry) (Mov rbx rdi) ; recv heap pointer (compile-e e '()) (Ret) (compile-defines ds) (Label 'raise_error_align) (Sub rsp 8) (Jmp 'raise_error))]))
It relies on a helper compile-defines for compiling each function definition and flattening the assembly instructions into a single list:
; [Listof Defn] -> Asm (define (compile-defines ds) (match ds ['() (seq)] [(cons d ds) (seq (compile-define d) (compile-defines ds))]))
Here’s an example of the code this compiler emits:
Examples
> (compile (parse '(define (double x) (+ x x)) '(double 5)))
(list
(Global 'entry)
(Label 'entry)
(Push 'rbx)
(Push 'r15)
(Mov 'rbx 'rdi)
(Lea 'rax 'ret8558)
(Push 'rax)
(Mov 'rax 80)
(Push 'rax)
(Jmp 'label_double_6334fa372629b92)
(Label 'ret8558)
(Pop 'r15)
(Pop 'rbx)
(Ret)
(Label 'label_double_6334fa372629b92)
(Mov 'rax (Mem 'rsp 0))
(Push 'rax)
(Mov 'rax (Mem 'rsp 8))
(Pop 'r8)
(Push 'r8)
(And 'r8 15)
(Cmp 'r8 0)
(Pop 'r8)
(Jne 'err)
(Push 'rax)
(And 'rax 15)
(Cmp 'rax 0)
(Pop 'rax)
(Jne 'err)
(Add 'rax 'r8)
(Add 'rsp 8)
(Ret)
(Label 'err)
(Mov 'r15 'rsp)
(And 'r15 8)
(Sub 'rsp 'r15)
(Extern 'raise_error)
(Call 'raise_error)
(Data)
(Label 'empty)
(Dq 0))
And we can confirm running the code produces results consistent with the interpreter:
Examples
> (exec (parse '(define (double x) (+ x x)) '(double 5))) 10
> (exec (parse '(define (tri x) (if (zero? x) 0 (+ x (tri (sub1 x))))) '(tri 9))) 45
> (exec (parse '(define (even? x) (if (zero? x) #t (odd? (sub1 x)))) '(define (odd? x) (if (zero? x) #f (even? (sub1 x)))) '(even? 101))) #f
The complete compiler code:
#lang racket (provide compile compile-e compile-es compile-define) ; for notes (provide rsp) (require "ast.rkt") (require "compile-ops.rkt") (require "types.rkt") (require a86/ast a86/registers) ;; Prog -> Asm (define (compile p) (match p [(Prog ds e) (prog (Global 'entry) (Label 'entry) (Push rbx) ; save callee-saved register (Push r15) (Mov rbx rdi) ; recv heap pointer (compile-e e '()) (Pop r15) ; restore callee-save register (Pop rbx) (Ret) (compile-defines ds) (Label 'err) pad-stack (Extern 'raise_error) (Call 'raise_error) (Data) (Label 'empty) (Dq 0))])) ;; [Listof Defn] -> Asm (define (compile-defines ds) (match ds ['() (seq)] [(cons d ds) (seq (compile-define d) (compile-defines ds))])) ;; Defn -> Asm (define (compile-define d) (match d [(Defn f xs e) (seq (Label (symbol->label f)) (compile-e e (reverse xs)) (Add rsp (* 8 (length xs))) ; pop args (Ret))])) ;; type CEnv = (Listof [Maybe Id]) ;; Expr CEnv -> Asm (define (compile-e e c) (match e [(Lit d) (compile-datum d)] [(Eof) (seq (Mov rax (value->bits eof)))] [(Var x) (compile-variable x c)] [(Prim0 p) (compile-prim0 p)] [(Prim1 p e) (compile-prim1 p e c)] [(Prim2 p e1 e2) (compile-prim2 p e1 e2 c)] [(Prim3 p e1 e2 e3) (compile-prim3 p e1 e2 e3 c)] [(If e1 e2 e3) (compile-if e1 e2 e3 c)] [(Begin e1 e2) (compile-begin e1 e2 c)] [(Let x e1 e2) (compile-let x e1 e2 c)] [(App f es) (compile-app f es c)])) ;; Datum -> Asm (define (compile-datum d) (cond [(string? d) (compile-string d)] [else (seq (Mov rax (value->bits d)))])) ;; String -> Asm (define (compile-string s) (let ((l (gensym 'string)) (n (string-length s))) (match s ["" (seq (Lea rax (Mem 'empty type-str)))] [_ (seq (Data) (Label l) (Dq (value->bits n)) (compile-string-chars (string->list s)) (if (odd? n) (Dd 0) (seq)) (Text) (Lea rax (Mem l type-str)))]))) ;; [Listof Char] -> Asm (define (compile-string-chars cs) (match cs ['() (seq)] [(cons c cs) (seq (Dd (char->integer c)) (compile-string-chars cs))])) ;; Id CEnv -> Asm (define (compile-variable x c) (let ((i (lookup x c))) (seq (Mov rax (Mem rsp i))))) ;; Op0 -> Asm (define (compile-prim0 p) (compile-op0 p)) ;; Op1 Expr CEnv -> Asm (define (compile-prim1 p e c) (seq (compile-e e c) (compile-op1 p))) ;; Op2 Expr Expr CEnv -> Asm (define (compile-prim2 p e1 e2 c) (seq (compile-e e1 c) (Push rax) (compile-e e2 (cons #f c)) (compile-op2 p))) ;; Op3 Expr Expr Expr CEnv -> Asm (define (compile-prim3 p e1 e2 e3 c) (seq (compile-e e1 c) (Push rax) (compile-e e2 (cons #f c)) (Push rax) (compile-e e3 (cons #f (cons #f c))) (compile-op3 p))) ;; Expr Expr Expr CEnv -> Asm (define (compile-if e1 e2 e3 c) (let ((l1 (gensym 'if)) (l2 (gensym 'if))) (seq (compile-e e1 c) (Cmp rax (value->bits #f)) (Je l1) (compile-e e2 c) (Jmp l2) (Label l1) (compile-e e3 c) (Label l2)))) ;; Expr Expr CEnv -> Asm (define (compile-begin e1 e2 c) (seq (compile-e e1 c) (compile-e e2 c))) ;; Id Expr Expr CEnv -> Asm (define (compile-let x e1 e2 c) (seq (compile-e e1 c) (Push rax) (compile-e e2 (cons x c)) (Add rsp 8))) ;; Id [Listof Expr] CEnv -> Asm ;; The return address is placed above the arguments, so callee pops ;; arguments and return address is next frame (define (compile-app f es c) (let ((r (gensym 'ret))) (seq (Lea rax r) (Push rax) (compile-es es (cons #f c)) (Jmp (symbol->label f)) (Label r)))) ;; [Listof Expr] CEnv -> Asm (define (compile-es es c) (match es ['() '()] [(cons e es) (seq (compile-e e c) (Push rax) (compile-es es (cons #f c)))])) ;; Id CEnv -> Integer (define (lookup x cenv) (match cenv ['() (error "undefined variable:" x)] [(cons y rest) (match (eq? x y) [#t 0] [#f (+ 8 (lookup x rest))])]))