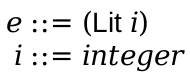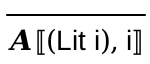6.1 Refinement, take one🔗

We’ve seen all the essential pieces—a grammar, an AST data type definition, a semantic specification (the interpreter), a compiler, etc.—for implementing a programming language, albeit for an amazingly simple language.

We will now, through a process of iterative refinement, grow the language to have an interesting set of features.

Our second language, which subsumes Abscond, is Blackmail. Expressions in Blackmail include integer literals and increment and decrement operations. It’s still a dead simple language, but at least programs do something.

6.2 Concrete syntax for Blackmail🔗

A Blackmail program consists of #lang racket line and a single expression, and the grammar of concrete expressions is:

So, 0, 120, and -42 are Blackmail expressions, but so are (add1 0), (sub1 120), (add1 (add1 (add1 -42))).

An example concrete program:

blackmail/add1-add1-40.rkt

#lang racket

(add1 (add1 40))

6.3 Abstract syntax for Blackmail🔗

The datatype for abstractly representing expressions can be defined as:

blackmail/ast.rkt

#lang racket

(provide Lit Prim1)

;; type Expr = (Lit Integer)

;;           | (Prim1 Op1 Expr)

;; type Op1 = 'add1 | 'sub1

(struct Lit (i) #:prefab)

(struct Prim1 (p e) #:prefab)

So, (Lit 0), (Lit 120), and (Lit -42) are Blackmail AST expressions, but so are (Prim1 'add1 (Lit 0)), (Sub1 (Lit 120)), (Prim1 'add1 (Prim1 'add1 (Prim1 'add1 (Lit -42)))).

The parser is more involved than Abscond, but still straightforward:

blackmail/parse.rkt

#lang racket

(provide parse)

(require "ast.rkt")

;; S-Expr -> Expr

(define (parse s)

(match s

[(? exact-integer?) (Lit s)]

[(list-rest (? symbol? k) sr)

(match k

[(? op1? o)

(match sr

[(list s1)

(Prim1 o (parse s1))]

[_ (error "op1: bad syntax" s)])]

[_ (error "parse error" s)])]

[_ (error "parse error" s)]))

(define (op1? x)

(memq x '(add1 sub1)))

Examples

> (parse '42)

'#s(Lit 42)

> (parse '(add1 42))

'#s(Prim1 add1 #s(Lit 42))

> (parse '(add1 (sub1 (add1 42))))

'#s(Prim1     add1     #s(Prim1 sub1 #s(Prim1 add1 #s(Lit 42))))

6.4 Meaning of Blackmail programs🔗

The meaning of a Blackmail program depends on the form of the expression:

• the meaning of an integer literal is just the integer itself,

• the meaning of an increment expression is one more than the meaning of its subexpression, and

• the meaning of a decrement expression is one less than the meaning of its subexpression.

To compute the meaning of an expression, the interp function does a case analysis of the expression:

blackmail/interp.rkt

#lang racket

(provide interp)

(require "ast.rkt")

(require "interp-prim.rkt")

;; Expr -> Integer

(define (interp e)

(match e

[(Lit i) i]

[(Prim1 p e)

(interp-prim1 p (interp e))]))

In the case of a (Prim1 p e) expression, the interpreter first recursively computes the meaning of the subexpression e and then defers to a helper function interp-prim1 which interprets the meaning of a given unary operation and value:

blackmail/interp-prim.rkt

#lang racket

(provide interp-prim1)

;; Op1 Integer -> Integer

(define (interp-prim1 op i)

(match op

['add1 (add1 i)]

['sub1 (sub1 i)]))

If the given operation is 'add1, the function adds 1; if it’s 'sub1, it subtracts 1.

We can write examples of the interp function, writing inputs in abstract syntax:

Examples

> (interp (Lit 42))
42
> (interp (Lit -7))
-7
> (interp (Prim1 'add1 (Lit 42)))
43
> (interp (Prim1 'sub1 (Lit 8)))
7
> (interp (Prim1 'add1 (Prim1 'add1 (Prim1 'add1 (Lit 8)))))
11

We could also write examples using concrete syntax, using the parser to construct the appropriate abstract syntax for us:

Examples

> (interp (parse '42))
42
> (interp (parse '-7))
-7
> (interp (parse '(add1 42)))
43
> (interp (parse '(sub1 8)))
7
> (interp (parse '(add1 (add1 (add1 8)))))
11

6.5 An Example of Blackmail compilation🔗

Just as we did with Abscond, let’s approach writing the compiler by first writing an example.

Suppose we want to compile (add1 (add1 40)). We already know how to compile the 40: (Mov 'rax 40). To do the increment (and decrement) we need to know a bit more a86. In particular, the Add instruction is relevant. It increments the contents of a register by some given amount.

So, a program that adds 1 twice to 40 looks like:

Examples

> (asm-interp     (prog (Global 'entry)           (Label 'entry)           (Mov 'rax 40)           (Add 'rax 1)           (Add 'rax 1)           (Ret)))

42

6.6 A Compiler for Blackmail🔗

To compile Blackmail, we make use of two more a86 instructions, Add and Sub. The compiler consists of two functions: the first, which is given a program, emits the entry point and return instructions, invoking another function to compile the expression:

blackmail/compile.rkt

#lang racket

(provide compile

compile-e)

(require "ast.rkt")

(require "compile-ops.rkt")

(require a86/ast a86/registers)

;; Expr -> Asm

(define (compile e)

(prog (Global 'entry)

(Label 'entry)

(compile-e e)

(Ret)))

;; Expr -> Asm

(define (compile-e e)

(match e

[(Lit i) (seq (Mov rax i))]

[(Prim1 p e) (compile-prim1 p e)]))

;; Op1 Expr -> Asm

(define (compile-prim1 p e)

(seq (compile-e e)

(compile-op1 p)))

Notice that compile-e is defined by structural recursion, much like the interpreter.

In the case of a unary primitive (Prim1 p e), the compiler first compiles the subexpression e obtaining a list of instructions that, when executed, will place e’s value in the 'rax register. After that sequence of instructions, the compiler emits instructions for carrying out the operation p, defering to a helper function compile-op1:

blackmail/compile-ops.rkt

#lang racket

(provide compile-op1)

(require "ast.rkt")

(require a86/ast a86/registers)

;; Op1 -> Asm

(define (compile-op1 p)

(match p

['add1 (Add rax 1)]

['sub1 (Sub rax 1)]))

This function either emits an Add or Sub instruction, depending upon p.

We can now try out a few examples:

Examples

> (compile-e (parse '(add1 (add1 40))))

(list (Mov 'rax 40) (Add 'rax 1) (Add 'rax 1))

> (compile-e (parse '(sub1 8)))

(list (Mov 'rax 8) (Sub 'rax 1))

> (compile-e (parse '(add1 (add1 (sub1 (add1 -8))))))

(list  (Mov 'rax -8)  (Add 'rax 1)  (Sub 'rax 1)  (Add 'rax 1)  (Add 'rax 1))

To see the complete code for these examples, we can use the compile function:

Examples

> (compile (parse '(add1 (add1 40))))

(list  (Global 'entry)  (Label 'entry)  (Mov 'rax 40)  (Add 'rax 1)  (Add 'rax 1)  (Ret))

> (compile (parse '(sub1 8)))

(list  (Global 'entry)  (Label 'entry)  (Mov 'rax 8)  (Sub 'rax 1)  (Ret))

> (compile (parse '(add1 (add1 (sub1 (add1 -8))))))

(list  (Global 'entry)  (Label 'entry)  (Mov 'rax -8)  (Add 'rax 1)  (Sub 'rax 1)  (Add 'rax 1)  (Add 'rax 1)  (Ret))

We can also run the code produced in these examples in order to see what they each produce:

Examples

> (asm-interp (compile (parse '(add1 (add1 40)))))

42

> (asm-interp (compile (parse '(sub1 8))))

7

> (asm-interp (compile (parse '(add1 (add1 (sub1 (add1 -8)))))))

-6

Based on this, it’s useful to define an exec function that (should) behave like interp, just as we did for Abscond:

blackmail/exec.rkt

#lang racket

(require a86/interp)

(require "compile.rkt")

(provide exec)

;; Expr -> Integer

(define (exec e)

(asm-interp (compile e)))

Examples

> (exec (parse '(add1 (add1 40))))

42

> (exec (parse '(sub1 8)))

7

> (exec (parse '(add1 (add1 (sub1 (add1 -8))))))

-6

This function will be the basis of our compiler correctness statement and a primary tool for testing the compiler.

And give a command line wrapper for parsing, checking, and compiling in compile-stdin.rkt, we can compile files as follows:

shell

> cat add1-add1-40.rkt | racket -t compile-stdin.rkt -m
        default rel
        section .text
        global $entry
$entry:
        mov rax, 40
        add rax, 1
        add rax, 1
        ret

And using the same Makefile setup as in Abscond, we capture the whole compilation process with a single command:

shell

> make add1-add1-40.run
make[1]: Entering directory '/home/runner/work/cmsc430.github.io/cmsc430.github.io/langs/blackmail'
cat add1-add1-40.rkt | racket -t compile-stdin.rkt -m > add1-add1-40.s
gcc -fPIC -c -g -o main.o main.c
gcc -fPIC -c -g -o print.o print.c
ld -r main.o print.o -o runtime.o
nasm -g -f elf64 -o add1-add1-40.o add1-add1-40.s
gcc runtime.o add1-add1-40.o -o add1-add1-40.run
rm add1-add1-40.o
make[1]: Leaving directory '/home/runner/work/cmsc430.github.io/cmsc430.github.io/langs/blackmail'
/usr/bin/ld: warning: add1-add1-40.o: missing .note.GNU-stack section implies executable stack
/usr/bin/ld: NOTE: This behaviour is deprecated and will be removed in a future version of the linker
> ./add1-add1-40.run
42

6.7 Correctness and random testing🔗

We can state correctness similarly to how it was stated for Abscond:

Compiler Correctness: For all e ∈ Expr and i ∈ Integer, if (interp e) equals i, then (exec e) equals i.

(This statement is actually identical to the statement of correctness for Abscond, however, it should be noted that the meaning of Expr, interp, exec refer to their Blackmail definitions.)

And we can test this claim by comparing the results of running compiled and interpreted programs, leading to the following property, which hopefully holds:

blackmail/correct.rkt

#lang racket

(provide check-compiler)

(require rackunit)

(require "interp.rkt")

(require "exec.rkt")

;; Expr -> Void

(define (check-compiler e)

(check-equal? (interp e)

(exec e)))

The problem, however, is that generating random Blackmail programs is less obvious compared to generating random Abscond programs (i.e. random integers). Randomly generating programs for testing is its own well studied and active research area. To side-step this wrinkle, we have provided a small utility for generating random Blackmail programs (random.rkt), which you can use, without needing the understand how it was implemented.

Examples

> (require "random.rkt")

> (random-expr)

'#s(Lit -1)

> (random-expr)

'#s(Prim1 sub1 #s(Lit 1))

> (random-expr)

'#s(Lit 1)

> (random-expr)

'#s(Prim1 add1 #s(Lit 4))

> (random-expr)

'#s(Prim1 sub1 #s(Lit 4))

> (define e (random-expr))

> e

'#s(Prim1     sub1     #s(Prim1        add1        #s(Prim1 add1 #s(Prim1 sub1 #s(Lit 1)))))

> (compile e)

(list  (Global 'entry)  (Label 'entry)  (Mov 'rax 1)  (Sub 'rax 1)  (Add 'rax 1)  (Add 'rax 1)  (Sub 'rax 1)  (Ret))

> (for ([i (in-range 10)])     (check-compiler (random-expr)))

6.8 A Broken Compiler🔗

It’s now probably time to acknowledge a short-coming in our compiler. Although it’s great that random testing is confirming the correctness of the compiler on specific examples, the compiler is unfortunately not correct in general. Neither was the Abscond compiler.

To see why, recall that integers in Blackmail are represented as 64-bit values in the compiled code. The problem arises when 64 bits isn’t enough. Since the run-time system interprets the 64-bit values as a signed integer, we have 1 bit devoted to the sign and 63 bits devoted to the magnitude of the integer. So the largest number we can represent is (sub1 (expt 2 63)) and the smallest number is (- (expt 2 63)). What happens if a program exceeds these bounds? Well, whatever x86 does. Let’s see:

Examples

> (define max-int (sub1 (expt 2 63)))
> (define min-int (- (expt 2 63)))
> (exec (Lit max-int))
9223372036854775807
> (exec (Prim1 'add1 (Lit max-int)))
-9223372036854775808
> (exec (Lit min-int))
-9223372036854775808
> (exec (Prim1 'sub1 (Lit min-int)))
9223372036854775807

Now there’s a fact you didn’t learn in grade school: in the first example, adding 1 to a number made it smaller; in the second, subtracting 1 made it bigger!

This problem doesn’t exist in the interpreter:

Examples

> (interp (Lit max-int))
9223372036854775807
> (interp (Prim1 'add1 (Lit max-int)))
9223372036854775808
> (interp (Lit min-int))
-9223372036854775808
> (interp (Prim1 'sub1 (Lit min-int)))
-9223372036854775809

So we have found a counter-example to the claim of compiler correctness:

Examples

> (check-compiler (Prim1 'add1 (Lit max-int)))

-------------------- FAILURE name:       check-equal? location:   /home/runner/work/cmsc430.github.io/cmsc430.github.io/langs/blackmail/correct.rkt:9:2 actual:     9223372036854775808 expected:   -9223372036854775808 --------------------

> (check-compiler (Prim1 'sub1 (Lit min-int)))

-------------------- FAILURE name:       check-equal? location:   /home/runner/work/cmsc430.github.io/cmsc430.github.io/langs/blackmail/correct.rkt:9:2 actual:     -9223372036854775809 expected:   9223372036854775807 --------------------

The problem also exists in Abscond in that we can write literals that exceed these bounds. The interpreter has no problem with such literals:

Examples

> (interp (Lit (add1 max-int)))

9223372036854775808

But the compiler will produce the wrong result:

Examples

> (exec (Lit (add1 max-int)))

-9223372036854775808

It’s also possible to exceed the bounds so thoroughly, that the program can’t even be compiled:

Examples

> (interp (Lit (expt 2 64)))

18446744073709551616

> (exec (Lit (expt 2 64)))

Mov: expects register, offset, or expression; given

18446744073709551616

The issue here being that a Mov instruction can only take an argument that can be represented in 64-bits.

What can we do? This is the basic problem of a program not satisfying its specification. We have two choices:

• change the spec (i.e. the semantics and interpreter)

• change the program (i.e. the compiler)

We could change the spec to make it match the behaviour of the compiler. This would involve writing out definitions that match the “wrapping” behavior we see in the compiled code. Of course if the specification is meant to capture what Racket actually does, taking this route would be a mistake. Even independent of Racket, this seems like a questionable design choice. Wouldn’t it be nice to reason about programs using the usual laws of mathematics (or at least something as close as possible to what we think of as math)? For example, wouldn’t you like know that (< i (add1 i)) for all integers i?

Unforunately, the other choice seems to paint us in to a corner. How can we ever hope to represent all possible integers in just 64 bits? We can’t. We need some new tricks. So in the meantime, our compiler is not correct, but writing down what it means to be correct is half the battle. We will get to correctness, but for the time being, we view the specification aspirationally.

6.9 Looking back, looking forward🔗

We’ve now built two compilers; enough to start observing a pattern.

Recall the phases of a compiler described in What does a Compiler look like?. Let’s identify these pieces in the two compilers we’ve written:

• Parsed into a data structure called an Abstract Syntax Tree

  • we use read to parse text into a s-expression

  • we use parse to convert an s-expression into an AST

• Checked to make sure code is well-formed

  • we don’t current do any, but more checking will come with more sophisticated langauges.

• Optimized into (equivalent) but faster program

  • we don’t do any yet

• Generated into assembly x86

  • we use compile to generate assembly (in AST form), and use asm-display to print concrete X86-64 code

• Linked against a run-time (usually written in C)

  • we link against our run-time written in main.c

Our recipe for building compiler involves:

1. Build intuition with examples,

2. Model problem with data types,

3. Implement compiler via type-guided-functions,

4. Validate compiler via tests.

As we move forward, the language we are compiling will grow. As the language grows, you should apply this recipe to grow the compiler along with the language.